The disc of a torsional pendulum has a moment of inertia of 600 k g ⋅ c m 2 kg \sdot cm^2 k g ⋅ c m 2 10 c m 10 \ cm 10 c m 40 c m 40 \ cm 40 c m 9 ° 9 \degree 9° 6 ° 6 \degree 6° 4 ° 4 \degree 4°
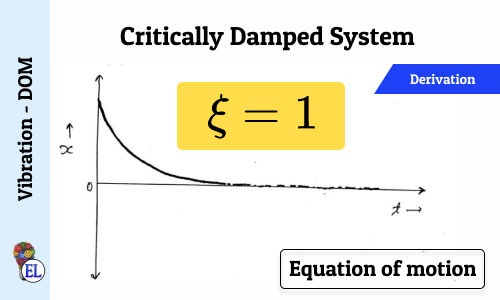
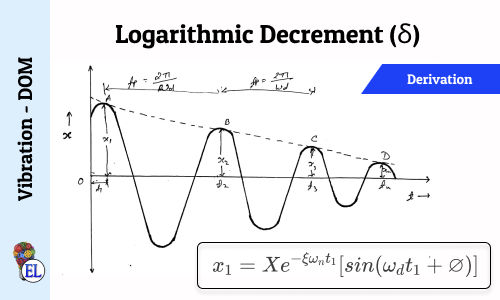
Logarithmic Decrement
Damping torque at unit velocity
The periodic time of vibration
Assume for the brass shaft, G = 4.4 ⨉ 1 0 10 N / m 2 G = 4.4⨉10^{10} N/m^2 G = 4.4⨉1 0 10 N / m 2
Solution
Given data:
Moment of inertia of disc, I = 600 k g ⋅ c m 2 = 600 × 1 0 − 4 k g ⋅ m 2 = 0.06 k g ⋅ m 2 Diameter of the shaft, d = 10 c m = 0.1 m Length of the shaft, L = 40 c m = 0.4 m Initial amplitude, x 0 = 9 ° Second amplitude, x 1 = 6 ° Third amplitude, x 2 = 4 ° \begin{aligned}
\text{Moment of inertia of disc,} \ \ I &= 600 \ kg \sdot cm^2 \\
&= 600 \times 10^{-4} \ kg \sdot m^2 \\
&= 0.06 \ kg \sdot m^2 \\
\\
\text{Diameter of the shaft,} \ \ d &= 10 \ cm = 0.1 \ m \\
\\
\text{Length of the shaft,} \ \ L &= 40 \ cm = 0.4 \ m \\
\\
\text{Initial amplitude,} \ \ x_0 &= 9 \degree \\
\\
\text{Second amplitude,} \ \ x_1 &= 6 \degree \\
\\
\text{Third amplitude,} \ \ x_2 &= 4 \degree \\
\end{aligned} Moment of inertia of disc, I Diameter of the shaft, d Length of the shaft, L Initial amplitude, x 0 Second amplitude, x 1 Third amplitude, x 2 = 600 k g ⋅ c m 2 = 600 × 1 0 − 4 k g ⋅ m 2 = 0.06 k g ⋅ m 2 = 10 c m = 0.1 m = 40 c m = 0.4 m = 9° = 6° = 4°
1. The logarithmic decrement:
δ = log e ( x 0 x 1 ) = log e ( 9 6 ) = log e ( 1.5 ) = 0.405 \begin{aligned}
\delta &= {\log}_e \bigg( {x_0 \over x_1}\bigg) \\
\\
&= {\log}_e \bigg( {9 \over 6}\bigg) \\
\\
&= {\log}_e (1.5) \\
\\
&= 0.405
\end{aligned} δ = log e ( x 1 x 0 ) = log e ( 6 9 ) = log e ( 1.5 ) = 0.405
2. Damping torque at unit velocity:
ξ = δ 4 π 2 + δ 2 = 0.405 4 π 2 + ( 0.405 ) 2 = 0.0642 \begin{aligned}
\xi &= {\delta \over \sqrt{4 {\pi}^2 + {\delta}^2}} \\
&= {0.405 \over \sqrt{4 {\pi}^2 + (0.405)^2}} \\
&= 0.0642
\end{aligned} ξ = 4 π 2 + δ 2 δ = 4 π 2 + ( 0.405 ) 2 0.405 = 0.0642
The torsional stiffness of shaft is,
K t = G J L = G ⋅ π 32 ⋅ ( d ) 4 L = 4.4 × 1 0 10 × π 32 ⋅ ( 0.1 ) 4 0.4 = 1.07 × 1 0 6 N m / r a d \begin{aligned}
K_t &= {GJ \over L} \\
\\
&= {G \sdot {\pi \over 32} \sdot (d)^4 \over L} \\
\\
&= {4.4 \times 10^{10} \times {\pi \over 32} \sdot (0.1)^4 \over 0.4} \\
\\
&= 1.07 \times 10^6 \ Nm/rad
\end{aligned} K t = L G J = L G ⋅ 32 π ⋅ ( d ) 4 = 0.4 4.4 × 1 0 10 × 32 π ⋅ ( 0.1 ) 4 = 1.07 × 1 0 6 N m / r a d
The natural circular frequency of system is,
ω n = K t I = 1.07 × 1 0 6 0.06 = 4242.5 r a d / s \begin{aligned}
{\omega}_n &= \sqrt{K_t \over I} \\
\\
&= \sqrt{1.07 \times 10^6 \over 0.06} \\
\\
&= 4242.5 \ \ rad/s
\end{aligned} ω n = I K t = 0.06 1.07 × 1 0 6 = 4242.5 r a d / s Now, Damping torque,
F t = c t ⋅ x ˚ F_t = c_t \sdot \mathring{x} F t = c t ⋅ x ˚ ∴ \therefore ∴ F t x ˚ = c t {F_t \over \mathring{x}} = c_t x ˚ F t = c t
Now, we know that;
ξ = c t c c \xi = {c_t \over c_c} ξ = c c c t ∴ c t = ξ ⋅ c c = ξ ( 2 ⋅ I ⋅ ω n ) = 0.0642 ( 2 × 0.06 × 4242.5 ) = 32.74 N ⋅ m ⋅ s / r a d \begin{aligned}
\therefore c_t &= \xi \sdot c_c \\
&= \xi (2 \sdot I \sdot {\omega}_n) \\
&= 0.0642(2 \times 0.06 \times 4242.5) \\
&= 32.74 \ \ N \sdot m \sdot s / rad
\end{aligned} ∴ c t = ξ ⋅ c c = ξ ( 2 ⋅ I ⋅ ω n ) = 0.0642 ( 2 × 0.06 × 4242.5 ) = 32.74 N ⋅ m ⋅ s / r a d
3. The time period of damped vibration:
t p = 2 π ω d = 2 π ω n 1 − ξ 2 = 2 π ( 4242.5 ) 1 − ( 0.0642 ) 2 = 0.00148 s e c o n d \begin{aligned}
t_p &= {2\pi \over {\omega}_d} \\
\\
&= {2\pi \over {\omega}_n \sqrt{1 - {\xi}^2}} \\
\\
&= {2\pi \over (4242.5) \sqrt{1 - (0.0642)^2}} \\
\\
&= 0.00148 \ \ second
\end{aligned} t p = ω d 2 π = ω n 1 − ξ 2 2 π = ( 4242.5 ) 1 − ( 0.0642 ) 2 2 π = 0.00148 seco n d
4. Frequency, if disc is removed from viscous fluid:
f n = ω n 2 π = 4242.5 2 π = 675.21 H z \begin{aligned}
f_n &= {{\omega}_n \over 2\pi} \\
\\
&= {4242.5 \over 2\pi} \\
\\
&= 675.21 \ Hz
\end{aligned} f n = 2 π ω n = 2 π 4242.5 = 675.21 Hz 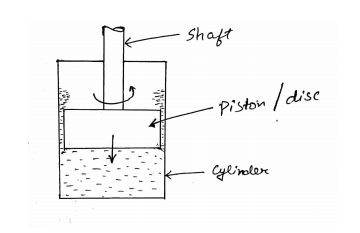


Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment