Law of Parallelogram of Forces : 5 in 5 MCQs S01-E01
Watch videoAs solved in the video under 5 minutes, this is the notes for the 5 MCQs solved with explanation. MCQ type questions are not only helpful for your examinations but also for competitive exams like GATE, UPSC and many more.
What is Law of Parallelogram of Forces?

Consider two forces and acting simultaneously on a particle as shown in the figure above. Let the angle between these two forces be . By extending imaginary lines from and , we can get a parallelogram as shown in the figure above as dotted lines.
Therefore, by the Law of Parallelogram of Forces the resultant of the forces and can be represented by the diagonal of this parallelogram and its direction as from force .
Definition of Law of Parallelogram of Forces
If two forces acting simultaneously on a particle are represented in magnitude and direction by the two sides of a parallelogram, then their resultant can be represented in magnitude and direction by the diagonal of the parallelogram which passes through their point of intersection.
And the magnitude of the resultant is given by:
And the direction of the resultant is given by:
Now, let's start solving MCQs. These questions will have 2 forces acting on a particle, hence we will apply the law of parallelogram of forces.
MCQ - 1
If , and and are acting along a same straight line, but in opposite direction. Then the resultant is?
a) c)
b) d)
Given:
(because P and Q are in straight line, but opposite in direction)
Answer: b

MCQ - 2
The resultant of two equal forces P making an angle of is:
a) c)
b) d)
Given:
Answer: b
MCQ - 3
The angle between two forces when resultant is maximum and minimum respectively is:
a) c)
b) d)
Explanation:
In the question it is asked to find the value of for the maximum value and the minimum value of .
We know that: .
Now if we change the value of and add or subtract it from the remaining value of and we get the value of .
So, to find the answer, let's take 4 extreme values from the unit circle as given in the options for
Now the values for these angles will be respectively.
Here, maximum value is (i.e. ) and minimum value is (i.e. ).
Therefore, at and at , the resultant will be maximum and minimum respectively.
Answer: a
MCQ - 4
The resultant of two forces each equal to P and acting at right angle is:
a) c)
b) d)
Given:
,
Answer: d
MCQ - 5
The resultant of two forces and is . If is doubled, the new resultant is perpendicular to P. Then,
a) c)
b) d)
Explanation:
We have two set of data here:
- Forces and , whose resultant is R
- If is doubled, then resultant(R') would be perpendicular to . This means and
This is only possible if:
Using the formula for resultant force:
Answer: c
Suggested Notes:
Variation of Tractive Force | Tractive Effort | Effect of Partial Balancing of Locomotives
Balancing of V-Engines
Concept of Direct and Reverse Crank for V-engines & Radial engines
Static and Dynamic Balancing
Multi Cylinder Inline Engine (with firing order) | Numerical
Critically Damped System (ξ = 1)
Damped free Vibration - Numerical 1
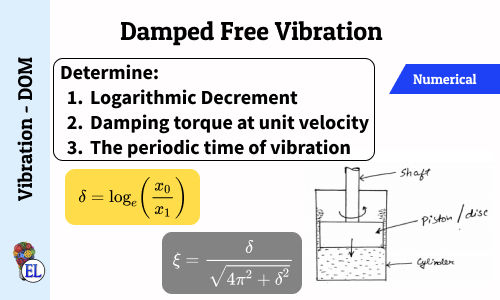
Damped free Vibration - Numerical 2

Damped free Vibration - Numerical 4
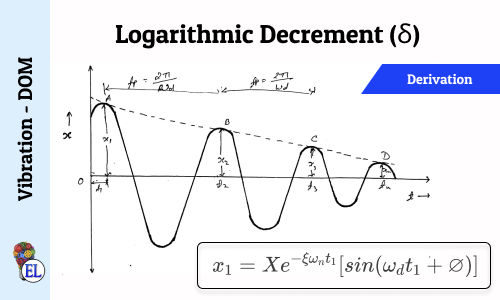
Logarithmic Decrement (δ)
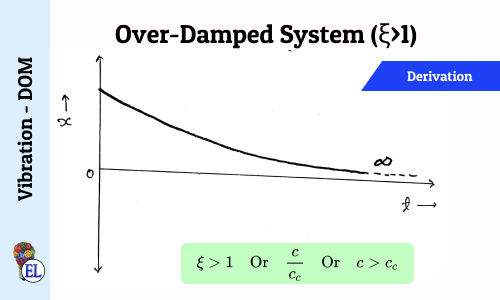
Over-Damped System (ξ>1)
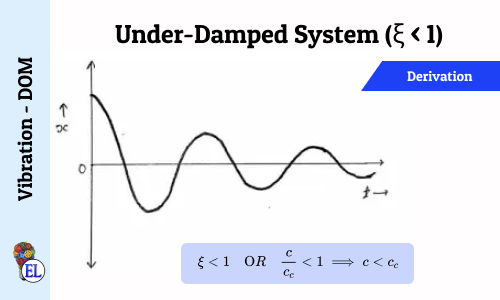
Under-Damped System (ξ < 1)

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment