Least Cost Method | Method to Solve Transportation Problem | Transportation Model
Watch videoLeast cost Method is one of the method to obtain feasible solution of Transportation Problem. We already understand the North West Corner Method | Method to Solve Transportation Problem | Transportation Model for transportation problem, to obtain feasible solution.
To understand Least Cost Method we will go through the numerical provided as follows (the same numerical we used in North West Corner Method | Method to Solve Transportation Problem | Transportation Model) :
Numerical
A mobile phone manufacturing company has three branches located in three different regions, say Jaipur, Udaipur and Mumbai. The company has to transport mobile phones to three destinations, say Kanpur, Pune and Delhi. The availability from Jaipur, Udaipur and Mumbai is 40, 60 and 70 units respectively. The demand at Kanpur, Pune and Delhi are 70, 40 and 60 respectively. The transportation cost is shown in the matrix below (in Rs). Use the Least Cost method to find a basic feasible solution (BFS).
Note that all the explanation is provided in “CYAN” colour. You have to write in examination the only thing which are given in this regular colour under each steps(if any), else you can directly solve matrix of the problem as explained here.
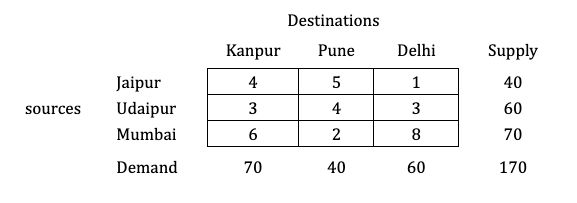
Solution:
Step 1: Balance the problem
Balance the problem meaning we need to check that if;
If this holds true, then we will consider the given problem as a balanced problem.
Now, what if it’s not balanced?
If such a condition occurs, then we have to add a dummy source or market; whichever makes the problem balanced.
You can watch a video on this type of numerical, which is known as Unbalanced Transportation Problems.
The given transportation problem is balanced.

Step 2: Select the lowest cost from the entire matrix and allocate the minimum of supply or demand.
We are using Least Cost Method here, so we will be indentifying the lowest cell value in this entire matrix.
Here, in this matrix we have 1 (For cell: Jaipur-Delhi) as the lowest value.

So, moving with that cell, and allocating the minimum of demand or supply, i.e. allocating 40 here (as supply value is 40, whereas demand is of 60).
Checking out the first row and not the last column, because we are allocating 40 in the cell for supply, as it is minimum.
Subtracting allocated value (i.e. 40) from corresponding supply and demand.
Step 3: Remove the row or column whose supply or demand is fulfilled and prepare a new matrix
As we have fulfilled the demand or supply for that row or column respectively, remove that row or column and prepare a new matrix, as shown below:
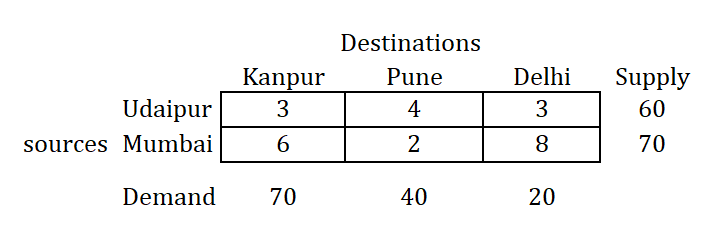
Step 4: Repeat the procedure until all the allocations are over
Repeat the same procedure of allocation of the smallest value in the new generated matrix and check out demand or supply based on the smallest value (of demand or supply) as shown below, until all allocations are over.
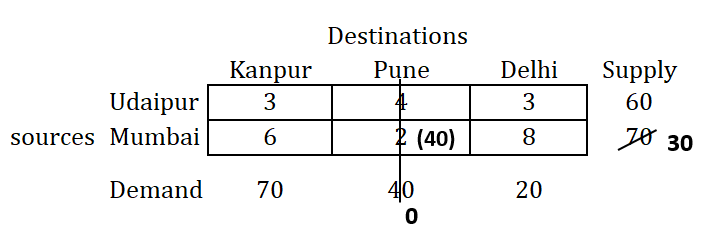
Tie in the following step!

You may find tie in selecting cell here in the above matrix, as we have minimun cell value 3 for two cells in the matrix above.
So whenever you find this kind of situation while evaluting matrix by Least Cost Method, you will have multiple solution to the problem, called alternate solutions.
The alternate solution of the this problem is provided at the end of this note-blog. In that we will be selecting the intersecting cell of Udaipur - Kanpur.
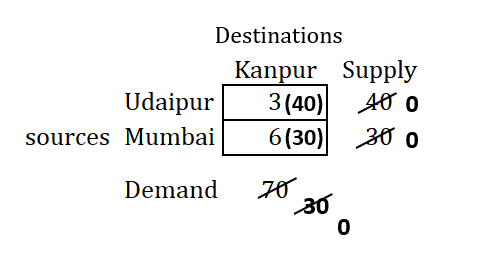
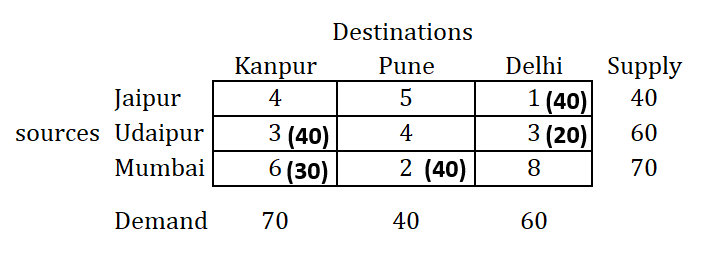
Step 5: After all the allocations are over, write the allocations and calculate the transportation cost
Once all allocations are over, prepare the table with all allocations marked and calculate the transportation cost as follows:
Alternate Solution
As we have tie in selecting minimum value at this step.
We can select any of this cell as mentioned earlier.
We have already seen above the solution by selecting minimum value as of Udaipur-Delhi intersecting cell, we will select now the another one and continuing the allocation using Least Cost Method as follows:
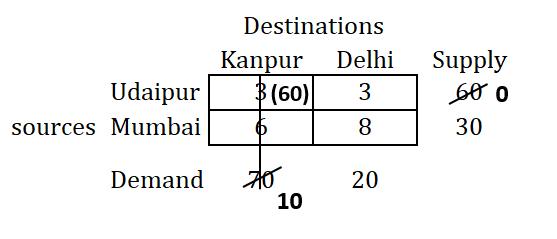
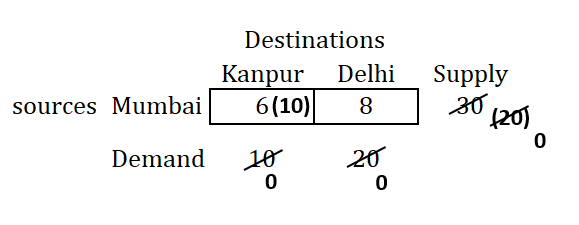

So, we will be having alternate solution as mentioned above, and alternate transportation cost as follows:
Thus, we have optimum Transportation cost as Rs. 480.
Find solution of same numerical by:
Suggested Notes:
Modified Distribution Method (MODI) | Transportation Problem | Transportation Model
Stepping Stone | Transportation Problem | Transportation Model
Vogel’s Approximation Method (VAM) | Method to Solve Transportation Problem | Transportation Model
Transportation Model - Introduction
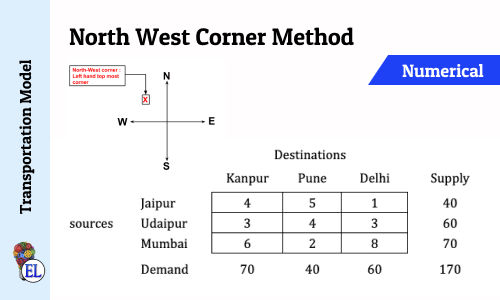
North West Corner Method | Method to Solve Transportation Problem | Transportation Model
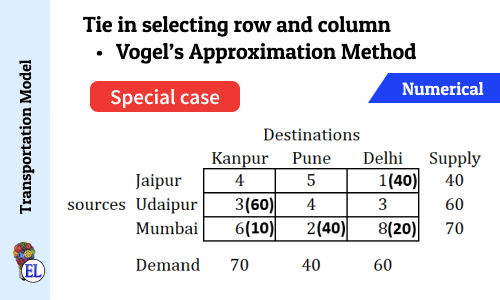
Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model
Assignment Model | Linear Programming Problem (LPP) | Introduction
Crashing Special Case - Multiple (Parallel) Critical Paths
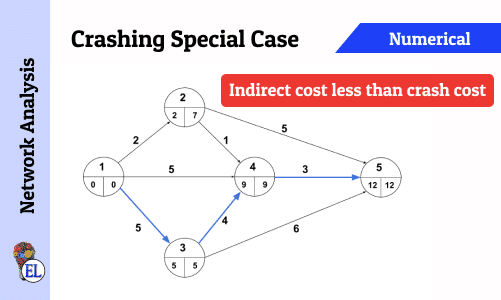
Crashing Special Case - Indirect cost less than Crash Cost

Basics of Program Evaluation and Review Technique (PERT)
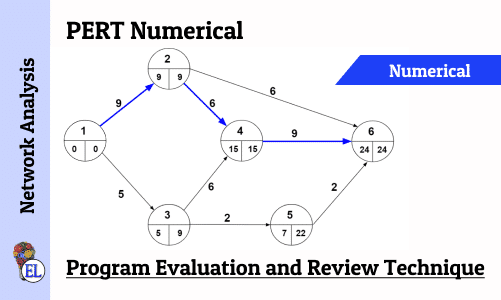
Numerical on PERT (Program Evaluation and Review Technique)
Network Analysis - Dealing with Network Construction Basics
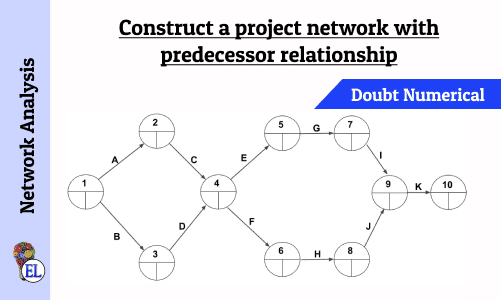
Construct a project network with predecessor relationship | Operation Research | Numerical
Graphical Method | Methods to solve LPP | Linear Programming
Basics of Linear Programming

Linear Programming Problem (LPP) Formulation with Numericals

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment