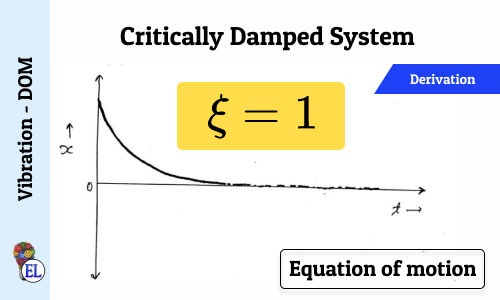
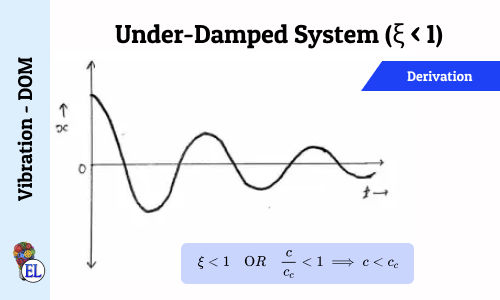
fig-1: displacement V/s time curve for under damped system
Logarithmic decrement
Logarithmic decrement is defined as the natural logarithm of the ratio of successive amplitude on the same side of mean position.
The rate of decay in the amplitudes of under-damped system is measured by the parameter known as logarithmic decrement.
Rate of decay in amplitudes depends on the amount of damping present in the system. So if the damping is more, then the rate of decay will also be more.
Let A and B are the two points on the successive cycles which shows maximum deflection as shown in figure.
The periodic time:
t p = t 2 − t 1 = 2 π ω d = 2 π ( 1 − ξ 2 ) ω n \begin{aligned}
t_p &= t_2 − t_1 \\
&= {2 \pi \over \omega_d} \\
&= {2 \pi \over \big(\sqrt {1-\xi^2}\big) \ \omega_n}
\end{aligned} t p = t 2 − t 1 = ω d 2 π = ( 1 − ξ 2 ) ω n 2 π The amplitude at time t 1 t_1 t 1 t 2 t_2 t 2
x 1 = X e − ξ ω n t 1 [ s i n ( ω d t 1 + ∅ ) ] x_1 = Xe^{-\xi \omega_n t_1} [sin(\omega_d t_1 + \varnothing)] x 1 = X e − ξ ω n t 1 [ s in ( ω d t 1 + ∅ )] And,
x 2 = X e − ξ ω n t 2 [ s i n ( ω d t 2 + ∅ ) ] ∴ x 2 = X e − ξ ω n ( t 1 + t p ) [ s i n { ω d ( t 1 + t p ) + ∅ } ] ∴ x 2 = X e − ξ ω n ( t 1 + t p ) [ s i n ( ω d t 1 + ω d t p + ∅ ) ] ∴ x 2 = X e − ξ ω n ( t 1 + t p ) [ s i n ( ω d t 1 + ω d ( 2 π ω d ) + ∅ ) ] ∴ x 2 = X e − ξ ω n ( t 1 + t p ) [ s i n ( ω d t 1 + 2 π + ∅ ) ] ∴ x 2 = X e − ξ ω n ( t 1 + t p ) [ s i n { 2 π + ( ω d t 1 + ∅ ) } ] ∴ x 2 = X e − ξ ω n ( t 1 + t p ) [ s i n ( ω d t 1 + ∅ ) ] \begin{aligned}
x_2 &= Xe^{-\xi \omega_n t_2} [sin(\omega_d t_2 + \varnothing)] \\
\therefore \quad x_2 &= Xe^{-\xi \omega_n (t_1 + t_p)} [sin \{ \omega_d (t_1 + t_p) + \varnothing \}] \\
\therefore \quad x_2 &= Xe^{-\xi \omega_n (t_1 + t_p)} [sin ( \omega_d t_1 + \omega_d t_p + \varnothing)] \\
\therefore \quad x_2 &= Xe^{-\xi \omega_n (t_1 + t_p)} [sin ( \omega_d t_1 + \omega_d \bigg({2 \pi \over \omega_d}\bigg) + \varnothing)] \\
\therefore \quad x_2 &= Xe^{-\xi \omega_n (t_1 + t_p)} [sin ( \omega_d t_1 + 2 \pi + \varnothing)] \\
\therefore \quad x_2 &= Xe^{-\xi \omega_n (t_1 + t_p)} [sin \{ 2 \pi + (\omega_d t_1 + \varnothing) \}] \\
\therefore \quad x_2 &= Xe^{-\xi \omega_n (t_1 + t_p)} [sin (\omega_d t_1 + \varnothing)] \\
\end{aligned} x 2 ∴ x 2 ∴ x 2 ∴ x 2 ∴ x 2 ∴ x 2 ∴ x 2 = X e − ξ ω n t 2 [ s in ( ω d t 2 + ∅ )] = X e − ξ ω n ( t 1 + t p ) [ s in { ω d ( t 1 + t p ) + ∅ }] = X e − ξ ω n ( t 1 + t p ) [ s in ( ω d t 1 + ω d t p + ∅ )] = X e − ξ ω n ( t 1 + t p ) [ s in ( ω d t 1 + ω d ( ω d 2 π ) + ∅ )] = X e − ξ ω n ( t 1 + t p ) [ s in ( ω d t 1 + 2 π + ∅ )] = X e − ξ ω n ( t 1 + t p ) [ s in { 2 π + ( ω d t 1 + ∅ )}] = X e − ξ ω n ( t 1 + t p ) [ s in ( ω d t 1 + ∅ )]
Now,
x 1 x 2 = X e − ξ ω n t 1 [ s i n ( ω d t 1 + ∅ ) ] X e − ξ ω n ( t 1 + t p ) [ s i n ( ω d t 1 + ∅ ) ] ∴ x 1 x 2 = e − ξ ω n ( t 1 − t 1 − t p ) ∴ x 1 x 2 = e ξ ω n t p \begin{aligned}
{x_1 \over x_2} &= {Xe^{-\xi \omega_n t_1} [sin(\omega_d t_1 + \varnothing)] \over Xe^{-\xi \omega_n (t_1 + t_p)} [sin (\omega_d t_1 + \varnothing)] }\\
\therefore \quad \quad {x_1 \over x_2} &= e^{-\xi \omega_n (t_1-t_1-t_p)} \\
\therefore \quad \quad {x_1 \over x_2} &= e^{\xi \omega_n t_p}
\end{aligned} x 2 x 1 ∴ x 2 x 1 ∴ x 2 x 1 = X e − ξ ω n ( t 1 + t p ) [ s in ( ω d t 1 + ∅ )] X e − ξ ω n t 1 [ s in ( ω d t 1 + ∅ )] = e − ξ ω n ( t 1 − t 1 − t p ) = e ξ ω n t p Now,logarithmic decrement is given by;
δ = l o g e ( x 1 x 2 ) ∴ δ = l o g e ( e ξ ω n t p ) ∴ δ = ξ ω n t p ∴ δ = ξ ω n 2 π ( 1 − ξ 2 ) ω n ∴ δ = 2 π ξ ( 1 − ξ 2 ) \begin{aligned}
\delta &= log_e \bigg({x_1 \over x_2}\bigg) \\
\therefore \quad \delta &= log_e (e^{\xi \omega_n t_p}) \\
\therefore \quad \delta &= \xi \omega_n t_p \\
\therefore \quad \delta &= \xi \omega_n {2 \pi \over \big(\sqrt {1-\xi^2}\big) \ \omega_n} \\
\therefore \quad \delta &= {2 \pi \xi\over \big(\sqrt {1-\xi^2}\big)}
\end{aligned} δ ∴ δ ∴ δ ∴ δ ∴ δ = l o g e ( x 2 x 1 ) = l o g e ( e ξ ω n t p ) = ξ ω n t p = ξ ω n ( 1 − ξ 2 ) ω n 2 π = ( 1 − ξ 2 ) 2 π ξ The logarithmic decrement can also be determined as follows;
δ = l o g e ( x 0 x 1 ) = l o g e ( x 1 x 2 ) = l o g e ( x 2 x 3 ) = … = l o g e ( x n − 1 x n ) Adding upto ’n’ terms n δ = l o g e ( x 0 x 1 ) + l o g e ( x 1 x 2 ) + l o g e ( x 2 x 3 ) + … + l o g e ( x n − 1 x n ) ∴ n δ = l o g e ( x 0 x 1 . x 1 x 2 . x 2 x 3 . … . x n − 1 x n ) Or n δ = l o g e ( x 0 x n ) ∴ δ = 1 n l o g e ( x 0 x n ) \begin{aligned}
\delta &= log_e \bigg({x_0 \over x_1}\bigg)= log_e \bigg({x_1 \over x_2}\bigg)= log_e \bigg({x_2 \over x_3}\bigg) = \dotso = log_e \bigg({x_{n-1} \over x_n}\bigg) \\
\text {Adding upto 'n' terms}\\
n\delta &= log_e \bigg({x_0 \over x_1} \bigg) + log_e \bigg({x_1 \over x_2}\bigg) + log_e \bigg({x_2 \over x_3}\bigg) + \dotso + log_e \bigg({x_{n-1} \over x_n}\bigg) \\
\therefore \ \ n\delta &= log_e \bigg({x_0 \over x_1} \ . {x_1 \over x_2} \ . {x_2 \over x_3} \ . \dots \ . {x_{n-1} \over x_n}\bigg) \\
\text {Or} \qquad \\
n\delta &= log_e \bigg({x_0 \over x_n}\bigg) \\
\therefore \quad \delta &= {1 \over n} log_e \bigg({x_0 \over x_n}\bigg)
\end{aligned} δ Adding upto ’n’ terms n δ ∴ n δ Or n δ ∴ δ = l o g e ( x 1 x 0 ) = l o g e ( x 2 x 1 ) = l o g e ( x 3 x 2 ) = … = l o g e ( x n x n − 1 ) = l o g e ( x 1 x 0 ) + l o g e ( x 2 x 1 ) + l o g e ( x 3 x 2 ) + … + l o g e ( x n x n − 1 ) = l o g e ( x 1 x 0 . x 2 x 1 . x 3 x 2 . … . x n x n − 1 ) = l o g e ( x n x 0 ) = n 1 l o g e ( x n x 0 ) where,x 0 x_0 x 0 x n x_n x n
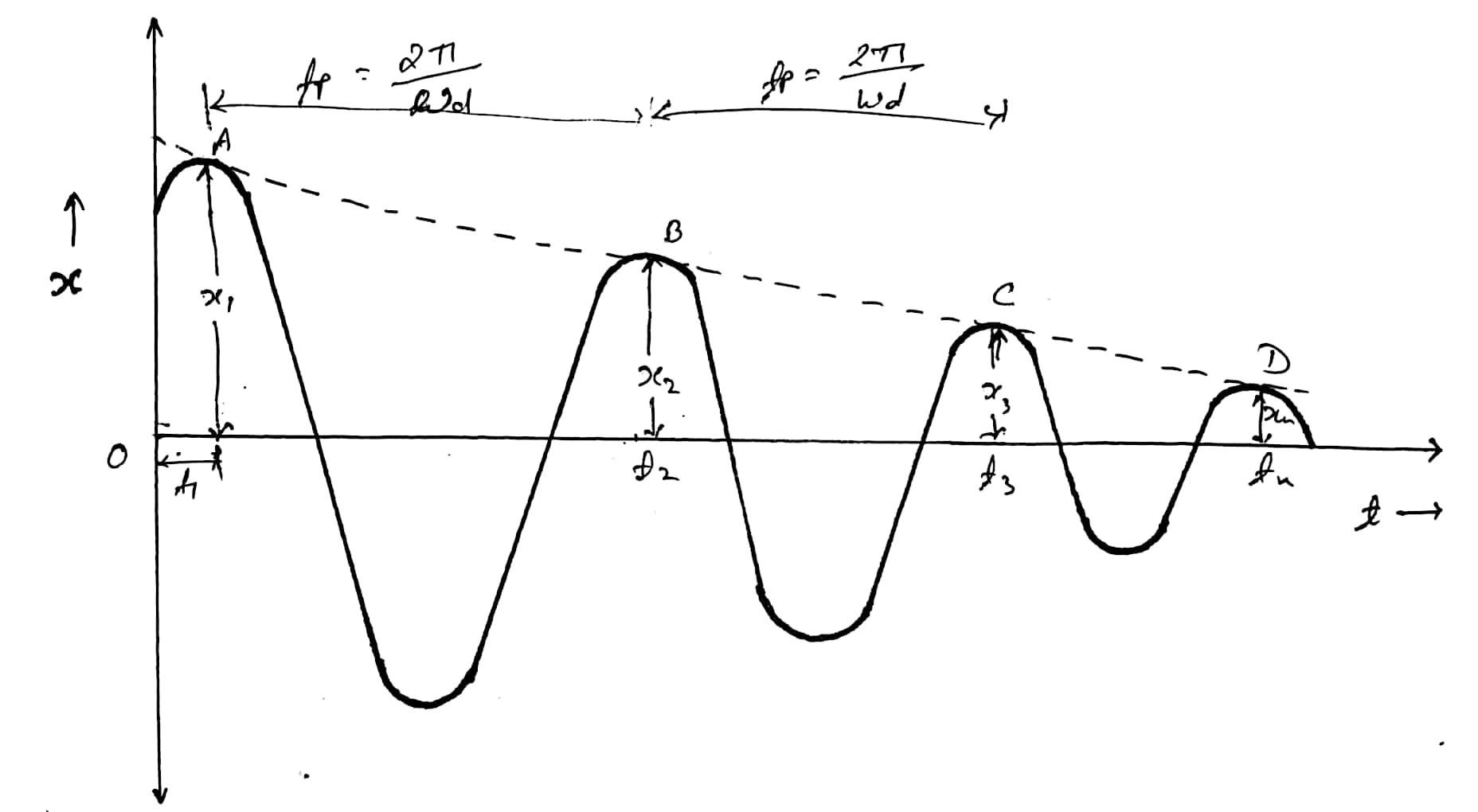 fig-1: displacement V/s time curve for under damped system
fig-1: displacement V/s time curve for under damped system

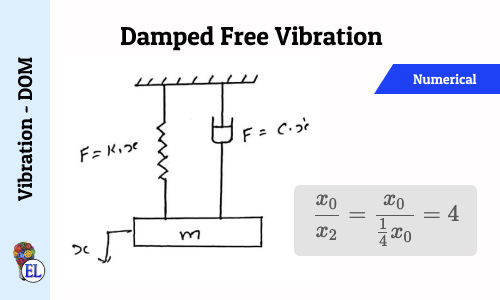
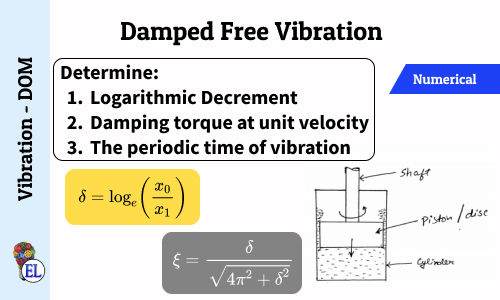
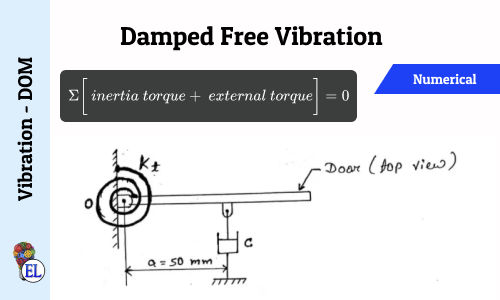

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment