Variation of Tractive Force | Tractive Effort | Effect of Partial Balancing of Locomotives
Watch videoWe have studied in earlier video that balancing is done on a locomotive. But because of balancing there are 3 effects that occurs on the locomotive, which are:
- Variation of tractive force
- Swaying couple
- Hammer blow
In this notes we will study the effect of variation of tractive force and also derive the equation to calculate the tractive force.
The first thing to remember here is that the Locomotive engines are reciprocating engines and we know that we cannot completely balance a reciprocating engine, we partially balance it. And partially balancing generates horizontal force and vertical force.
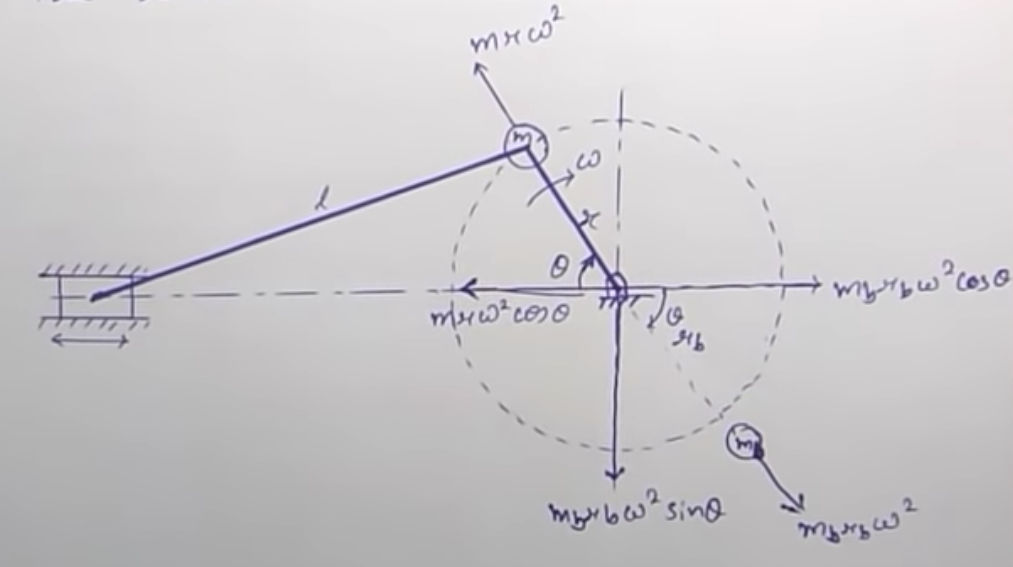 Image from video Balancing of Reciprocating Masses [Part-2] | Partial balancing | (Dynamics of Machinery)
Image from video Balancing of Reciprocating Masses [Part-2] | Partial balancing | (Dynamics of Machinery)
In the video of partial balancing of reciprocating of engines ( Video Part-1 & Video Part-2 ) we have studied that the unbalanced force acting in horizontal and vertical direction is given by:
Now, let us imagine the horizontal force in three dimensions by looking at this diagram
 Unbalanced horizontal force acting on cylinders of locomotive
Unbalanced horizontal force acting on cylinders of locomotive
In the above diagram, let's represent the horizontal unbalanced force acting on cylinder 1 as and similarly the horizontal unbalanced force acting on cylinder 2 as .
From this, it becomes easier to understand what is traction force. It is the resultant of the two horizontal unbalanced force. Hence we get the following equation:

Traction force definition
The resultant unbalanced horizontal force due to the two cylinder along the line of stroke of cylinder is called traction force.
Remember:
Try to write the definition by explaining the things that we did in the calculation. This way it becomes easier for you to understand it.
Now for cylinder 1, and using equation (1) from above, we can say that:
Similarly for cylinder 2:
As we have studied in the last video, if cylinder 1 angle is at then the cylinder 2 angle will be at . Therefore from equation (4) we can say that:
From equation (2)
Now we need to find the maximum and minimum of this tractive force. To do this we need to differentiate equation (6) with respect to the variables. Here our variable is . So we need to differentiate with respect to .
Doing this we get:
Therefore, we get or .
Now we will put the value of both these in equation (6) to find the variation of tractive force.
For we get,
Similarly for we get,
Since we get the maximum and minimum value of tractive force, we can say that the value of varies between to .
Which we can represent as:
Suggested Notes:

Law of Parallelogram of Forces : 5 in 5 MCQs S01-E01
Balancing of V-Engines
Concept of Direct and Reverse Crank for V-engines & Radial engines
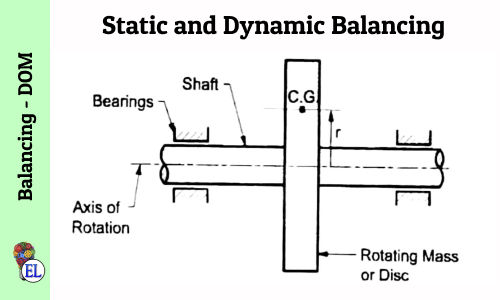
Static and Dynamic Balancing
Multi Cylinder Inline Engine (with firing order) | Numerical
Critically Damped System (ξ = 1)
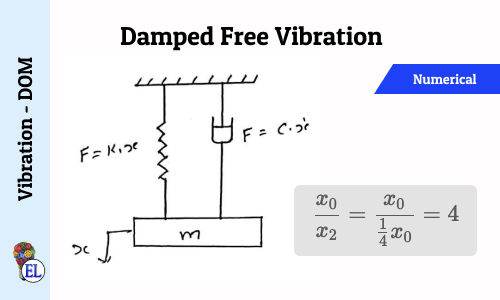
Damped free Vibration - Numerical 1
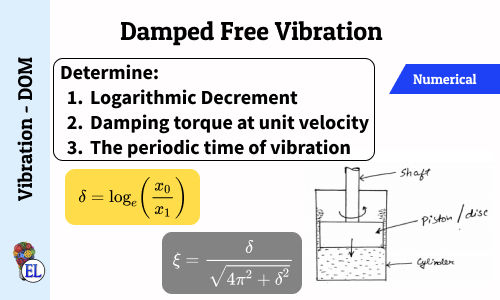
Damped free Vibration - Numerical 2

Damped free Vibration - Numerical 4
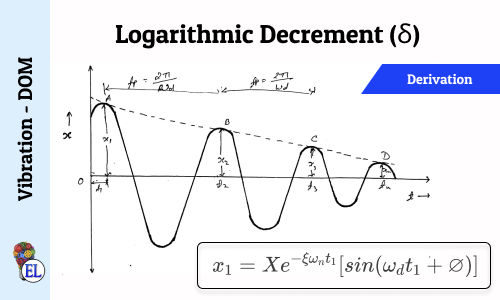
Logarithmic Decrement (δ)
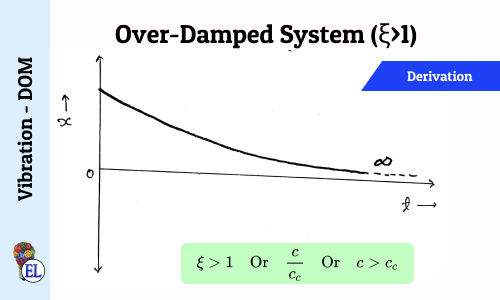
Over-Damped System (ξ>1)
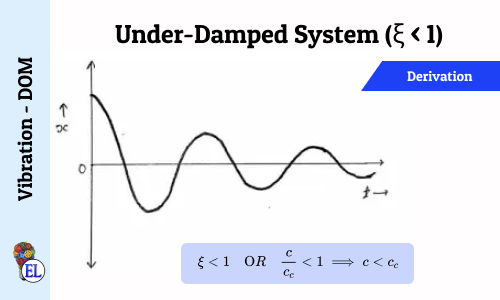
Under-Damped System (ξ < 1)

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment