Transportation Model - Introduction
Watch videoWhat is the Transportation Model?
Click here to know about Methods to solve Transportation Model Problem provided below here in notes ↓
-
Transportation Model is a special case of LPP(Linear Programming Problem) in which the main objective is to transport a product from various sources to various destinations at total minimum cost.
-
In Transportation Models, the sources and destinations are known, the supply and demand at each source and destinations are also known.
-
It is designed to find the best arrangement for transportation such that the transportation cost is minimum.
For example:
-
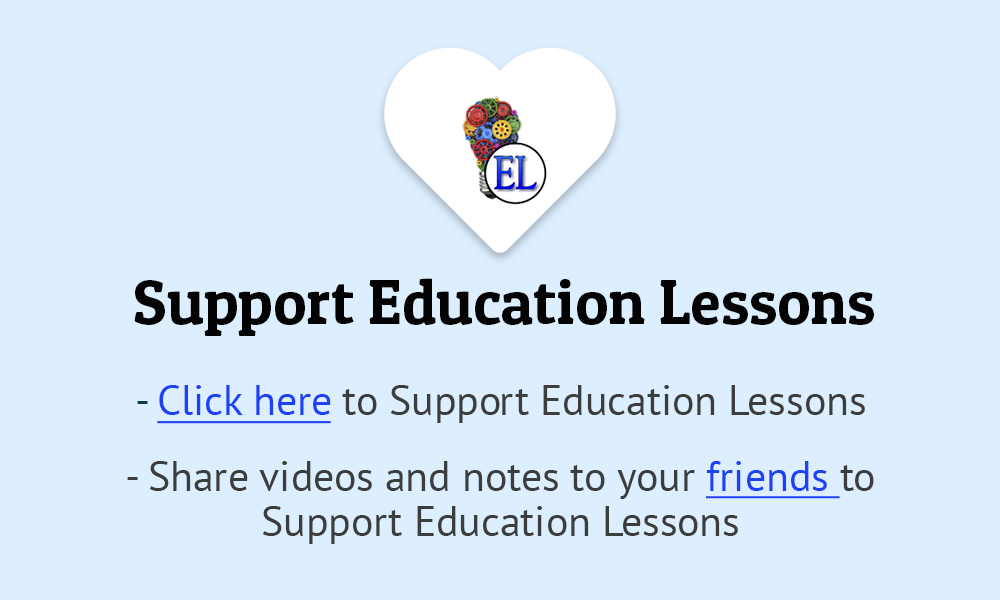
Consider three companies (Company1, Company2 and Company3) which produce mobile phones and are located in different regions.
-
Similarly, consider three cities (namely CityA, CityB & CityC) where the mobile phones are transported.
-
The companies where mobile phones are available are known as sources and the cities where mobile phones are transported are called destinations.
-
Let,
Company1 produces a1 units,
Company2 produces a2 units,
Company3 produces a3 units. -
Let,
demand in CityA is b1 units,
demand in CityB is b2 units,
demand in CityC is b3 units. -
The cost of transportation from each source to destination is given in table
- The transportation of mobile phones should be done in such a way that the total transportation cost is minimum.

Types of transportation problems:
- There are two types of transportation problems:
i) Balanced transportation problem: The sum of supply and sum of demand are same.
ii) Unbalanced transportation problem: The sum of supply and sum of demand are different.
Methods to solve Transportation Model
Industrial applications of Transportation Model
- Minimize the transportation cost from source to destination.
- Determine lowest cost location for new industries, offices, warehouse, etc.
- Determine the number of products to be manufactured according to demand.
- Courier Services: Helps in taking proper decisions to find the best route for transportation.
Suggested Notes:
Modified Distribution Method (MODI) | Transportation Problem | Transportation Model
Stepping Stone | Transportation Problem | Transportation Model
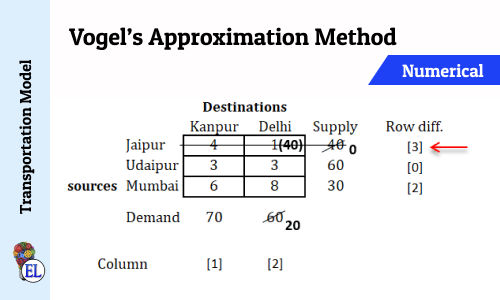
Vogel’s Approximation Method (VAM) | Method to Solve Transportation Problem | Transportation Model
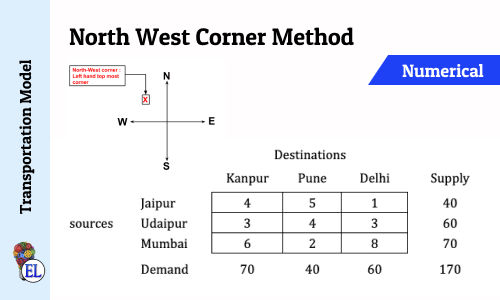
North West Corner Method | Method to Solve Transportation Problem | Transportation Model
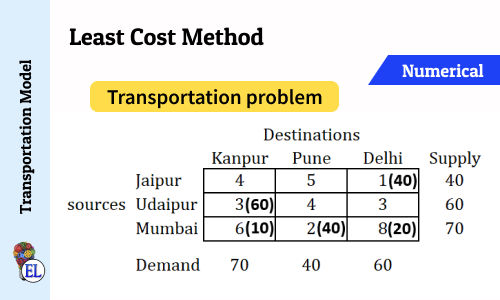
Least Cost Method | Method to Solve Transportation Problem | Transportation Model
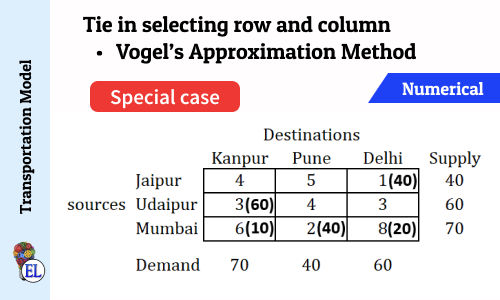
Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model

Assignment Model | Linear Programming Problem (LPP) | Introduction

Crashing Special Case - Multiple (Parallel) Critical Paths

Crashing Special Case - Indirect cost less than Crash Cost

Basics of Program Evaluation and Review Technique (PERT)

Numerical on PERT (Program Evaluation and Review Technique)

Network Analysis - Dealing with Network Construction Basics

Construct a project network with predecessor relationship | Operation Research | Numerical
Graphical Method | Methods to solve LPP | Linear Programming
Basics of Linear Programming

Linear Programming Problem (LPP) Formulation with Numericals

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment