Damped free Vibration - Numerical 4
Watch videoComments
Numerical: A door along with door-closing system shown is shown in the figure below. It has a moment of inertia of about the hinge axis. If the stiffness of torsional spring is , find the most suitable value of the damping coefficient.
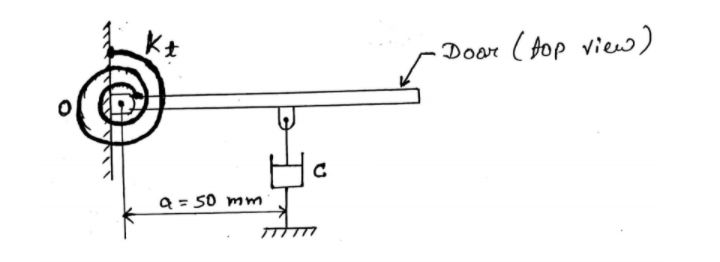
Solution:
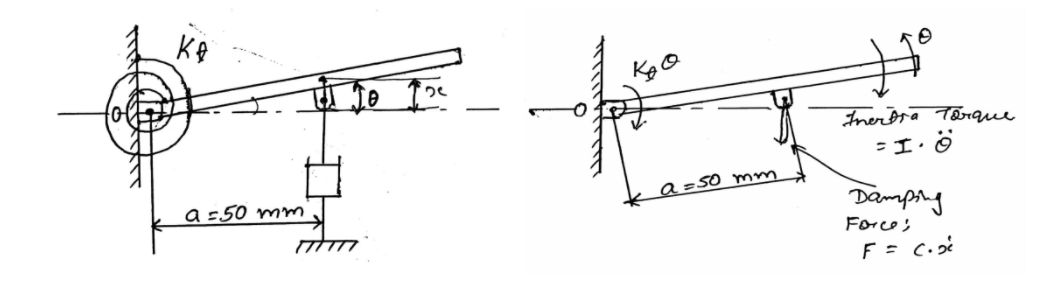
Given data:
Moment of inertia,
Stiffness of torsional spring
According to D'Alembert's principle;

The above equation can be written as:
Now,
Suggested Notes:
Law of Parallelogram of Forces : 5 in 5 MCQs S01-E01
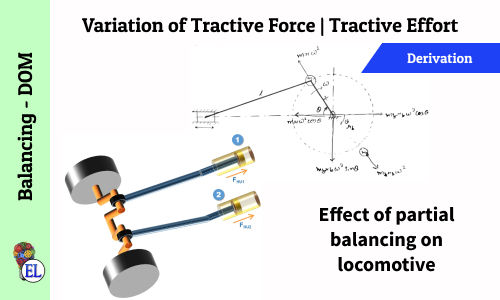
Variation of Tractive Force | Tractive Effort | Effect of Partial Balancing of Locomotives
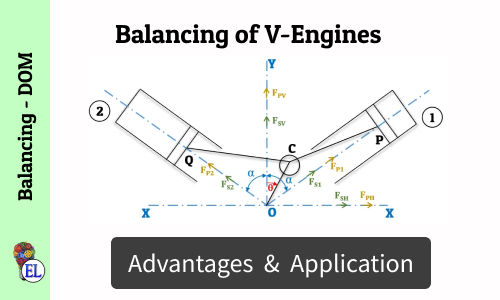
Balancing of V-Engines
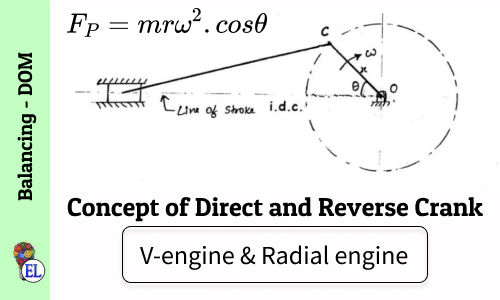
Concept of Direct and Reverse Crank for V-engines & Radial engines
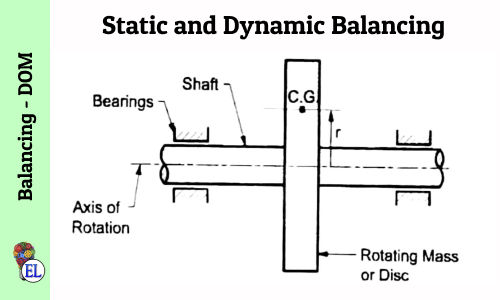
Static and Dynamic Balancing
Multi Cylinder Inline Engine (with firing order) | Numerical
Critically Damped System (ξ = 1)
Damped free Vibration - Numerical 1
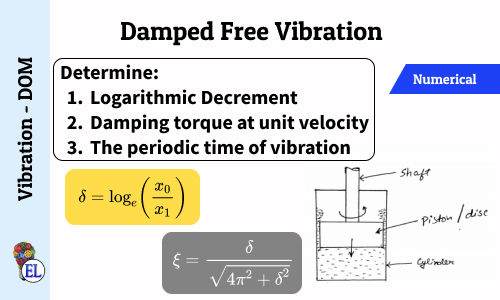
Damped free Vibration - Numerical 2
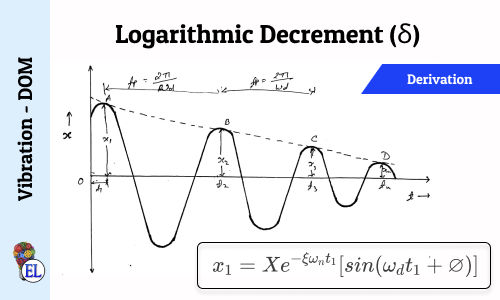
Logarithmic Decrement (δ)
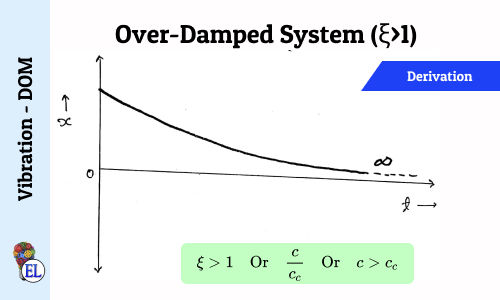
Over-Damped System (ξ>1)
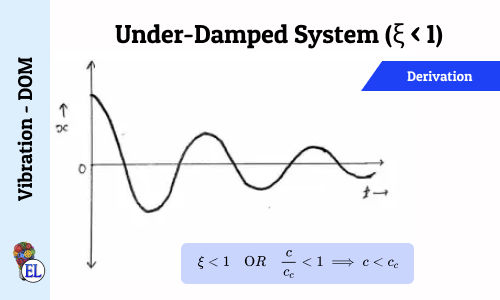
Under-Damped System (ξ < 1)

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment