Basics of Linear Programming
Watch videoHistory
At the time of World War- II, G.B. Dantzing was working with US Air force and he was facing many problems such as allocation of weapons to different war locations, military logistics, etc. Since available resources are limited (restricted), it was very crucial to allocate optimum number of weapons or logistics in order to fulfil the objective of winning the war. At that time, he developed the technique to solve such problems, and that technique is known as Linear Programming (LP).
Linear Programming
LP consists of two words – Linear and Programming. Linear word represents that relationship between variables is linear. Programming represents mathematical modelling and development of algorithms to solve a problem that involves optimum allocation of limited or restricted resources.
Definition
-
Linear Programming is a mathematical modelling for optimization of a function (Objective Function), subject to restricted resources of variables (represented ‘n’ form of linear equations and/or inequalities).
-
Objective function may be to maximize profit or to minimize loss or any other measures which to be obtained in the best optimal manner. Constraints are restrictions on available man hours, materials, money, machines, etc.
In general, if the resources are unlimited, then there will not need to define any kind of strategy. Since, resources are limited, there should be a well-defined strategy.
Pre-requirements of LP
- Decision variables should be interrelated and non-negative. Decision variables are those variables which are decided at the starting of solving the sum.
- There must be a well-defined objective function, which can be represented as a linear function of decision variables.
- There must be constraints on amount of resources which can be expressed as linear inequalities in terms of decision variables.
Properties/Assumptions of LP
Tip: As suggested in video, properties of LP can be easily remembered as keyword .
Proportionality:
The amount of each resource consumed and its contribution to profit in objective function must be proportional to the value of each decision variable. For eg: If one egg can provide 8 g of protein, then 10 eggs can provide 80 g (10X8=80 g) of protein.
Additivity:
The total value of the objective function equals the sum of the contribution of each variable to the objective function. Similarly, total resource use is the sum of the resource use of each variable. For eg: Total profit by selling ‘n’ products must be equal to the profit earned by selling the items individually. On the other hand, the total cost of manufacturing ‘n’ products at a time, must be equal to the cost of manufacturing items individually.
Non-negativity:
It is assumed that values of decision variables are either positive or zero. It cannot be negative.
Continuity:
It is assumed that the solution value of decision variables and the amount of resources used are not be integer values. For eg: It is not possible to have 3.5 as the optimum number of products.
Certainty of coefficients:
In all LP models, the coefficients of objective function, R.H.S. coefficients of constraints and resources values are certainly and precisely known and measurable. Also, it is assumed that those values remain constant irrespective of time.
Advantages of LP:
- Optimum allocation of resources: LP shows the allocation of resources to fulfil the objective function and helps in making the optimum use of available resources.
- Improvement in quality of decision: LP improves decision quality as it gives accurate values of decision variables to fulfil the objective function.
- Exploring bottleneck machines: Bottleneck machines are those machines which cannot meet the demand and because of them other machines are idle. LP model identifies this bottleneck machines and explores the problem of low production capacity of the plant.
- Re-evaluation of basic plan: LP re-evaluates the basic plan as per changing conditions. If condition change when the plan is partly carried out, they can be determined so as to adjust the remainder of the plan for best result.

Limitations of LP:
- LP treats relationships between variables as Linear. However, always it is not possible to have linearity.
- LP assumes that outcome of problem has decision variables as integers.
- LP assumes the certainty of the coefficients, but in each case it is not possible to determine the values of coefficients.
- LP deals with single objective functions, where as in real life situation business may have multiple objectives.
- LP ignores the effect of time.
Applications of LP:
Now-a-days, LP has wide applications in different sectors like industrial, management, farming, financial and many other miscellaneous applications.
1) Product Management:
- Product Mix: Company produces number of products from same limited production resources. In such cases it is essential to determine the quantity of each product to be manufactured knowing the profit induced and amount of materials consumed by each of them. The objective is to maximize profit subject to all constraints. For example, wafer manufacturing companies like Balaji.
 Image source: http://www.walkthroughindia.com/
Image source: http://www.walkthroughindia.com/
- Blending problems: When a product can be made from a variety of raw materials, each of which has a particular composition and price. The objective here is to determine the minimum cost blend subject to availability of the raw materials and the minimum constraints on certain product constituents.
For example, we are producing some product-X, and for which we have four different raw materials- A, B, C & D. Now, product-X can be made of A blend with B, as well as B with D and A with C. Now, for each particular raw material has different price, so compositions have their different price too. LP helps in selecting optimum composition and its price, subjected to constraints.
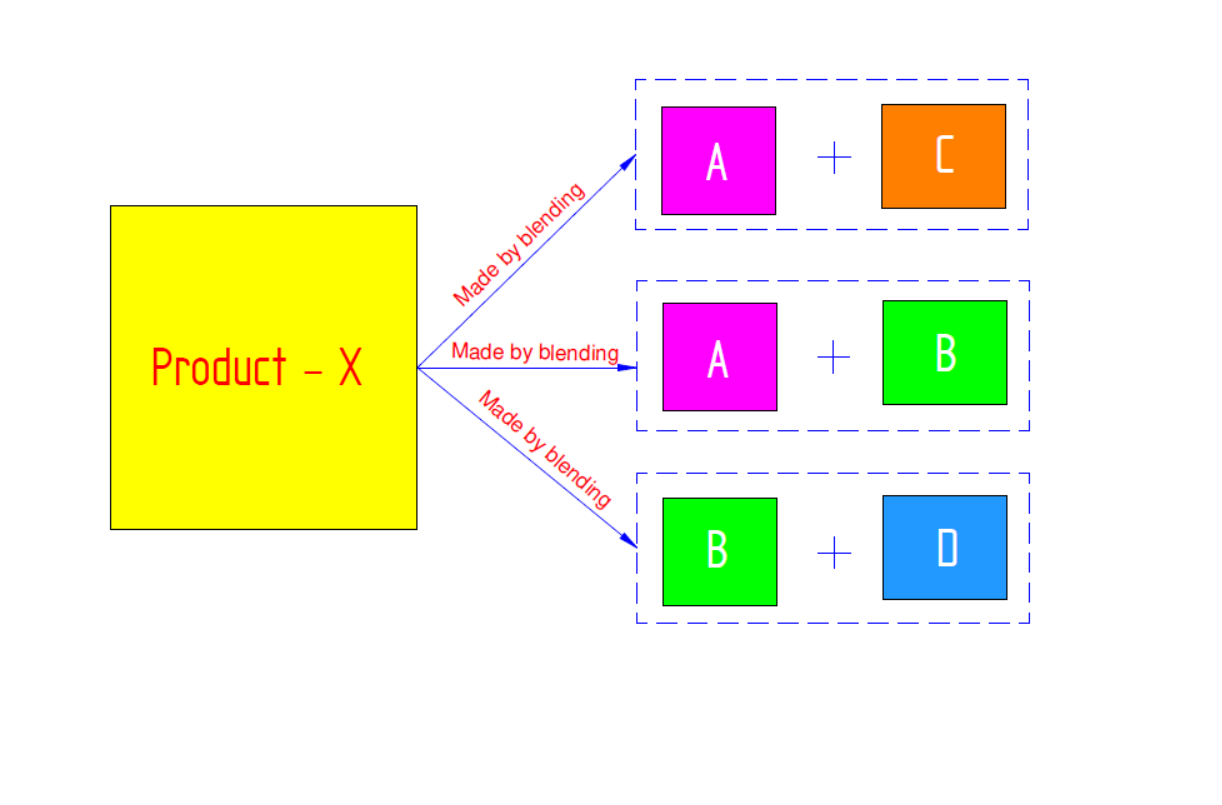 Image illustrating Blending Problem
Image illustrating Blending Problem
- Trim loss: When an item can be made of standard size (like glass, paper,sheet, etc.), the problem that arises is to determine which combination of requirements should be produced from standard materials in order to minimize the trim loss (wastage).
- Production Planning: This deals with the determination of minimum cost production plan over a planning period of an item with a fluctuating demand considering the initial number of units in inventory, production capacity,constraints on production, manpower and all relevant cost factors. The objective here is to minimize total operational costs.
2) Marketing Management:
- Media selection: LP techniques can helps in determining the advertising media mix so as to maximize the effective exposure, subject to limitation of budget, specified exposure rates to different market segments, specified minimum and maximum number of advertisements in various media.
- Travelling salesman problem: The problem of salesman is to find the shortest route starting from a given city, visiting each specified cities and then returning to the original point of departure, provided no city shall be visited twice during the tour.
- Physical distribution: LP determines the most economic and efficient manner of locating manufacturing plants and distribution centers for physical distribution.
3) Agricultural Applications:
- Farm management: LP can be applied in agricultural planning like allocation of limited resources such as available land, labour, water supply and working capital, etc. in such a way so as to maximize net revenue.
4) Financial Management:
- Capital budgeting problems: This deals with the selection of specific investment activity among several other activities.
- Profit planning: This deals with the maximization of profit margin from investment in plant facilities and equipment, cash on hand and inventory.
5) Miscellaneous problems:
- Diet problems: Diet problem includes the optimization of food quantities in order to fulfil the nutrition proportions as well as to minimize the cost of the food. Dieticians can use LP for planning a balance diet for a particular patient.
- Inspection problems: These problems relates with the deciding the optimum number of inspectors in order to inspect the raw materials. Also, the cost of inspectors should be minimum and reliability requires being high. This helps in deciding the optimum time to move on machine inspection based on require output, so as to increase the profit by decreasing the manufacturing time of particular product.
- Military Applications: Military application includes the problem of allocation of limited tools and technologies to various locations.
Suggested Notes:
Modified Distribution Method (MODI) | Transportation Problem | Transportation Model
Stepping Stone | Transportation Problem | Transportation Model
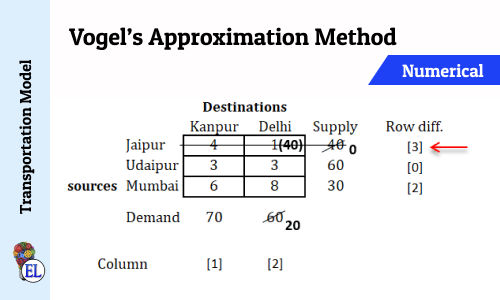
Vogel’s Approximation Method (VAM) | Method to Solve Transportation Problem | Transportation Model

Transportation Model - Introduction
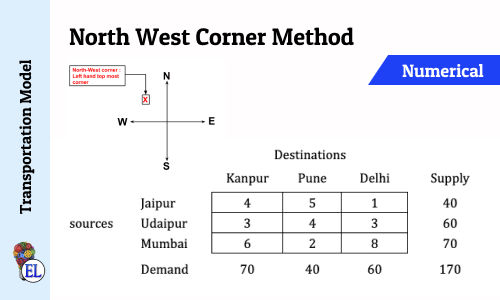
North West Corner Method | Method to Solve Transportation Problem | Transportation Model
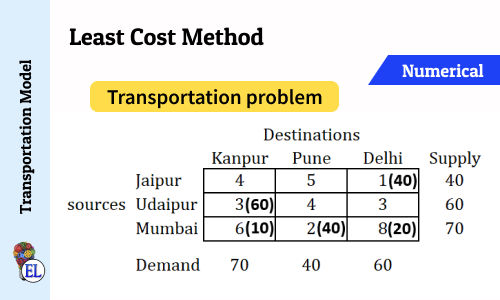
Least Cost Method | Method to Solve Transportation Problem | Transportation Model
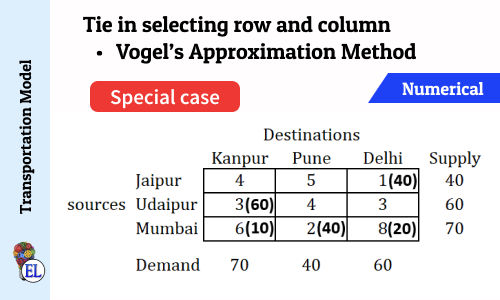
Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model

Assignment Model | Linear Programming Problem (LPP) | Introduction

Crashing Special Case - Multiple (Parallel) Critical Paths

Crashing Special Case - Indirect cost less than Crash Cost

Basics of Program Evaluation and Review Technique (PERT)

Numerical on PERT (Program Evaluation and Review Technique)

Network Analysis - Dealing with Network Construction Basics

Construct a project network with predecessor relationship | Operation Research | Numerical
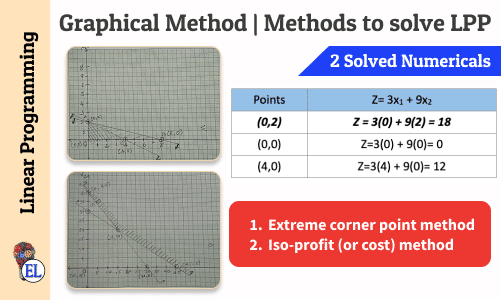
Graphical Method | Methods to solve LPP | Linear Programming

Linear Programming Problem (LPP) Formulation with Numericals

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment