Assignment Model | Linear Programming Problem (LPP) | Introduction
Watch videoWhat is Assignment Model?
→ Assignment model is a special application of Linear Programming Problem (LPP), in which the main objective is to assign the work or task to a group of individuals such that;
i) There is only one assignment.
ii) All the assignments should be done in such a way that the overall cost is minimized (or profit is maximized, incase of maximization).
→ In assignment problem, the cost of performing each task by each individual is known.
→ It is desired to find out the best assignments, such that overall cost of assigning the work is minimized.
For example:
-
Suppose there are 'n' tasks, which are required to be performed using 'n' resources.
-
The cost of performing each task by each resource is also known (shown in cells of matrix)
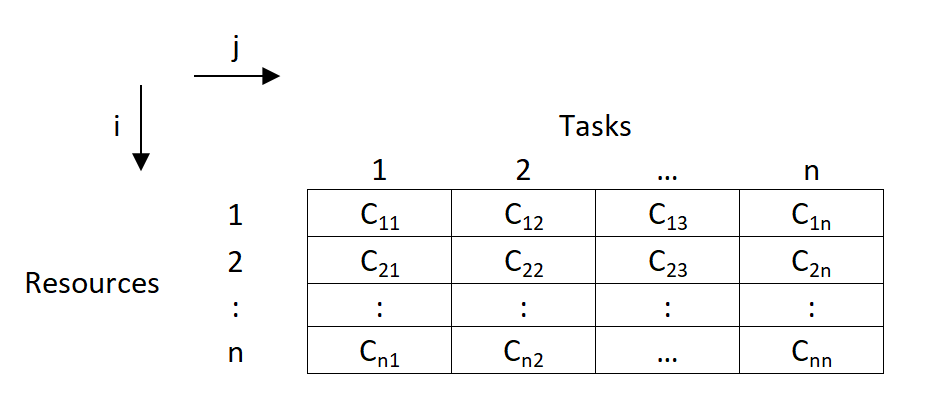
- In the above asignment problem, we have to provide assignments such that there is one to one assignments and the overall cost is minimized.
How Assignment Problem is related to LPP?
OR
Write mathematical formulation of Assignment Model.
→ Assignment Model is a special application of Linear Programming (LP).
→ The mathematical formulation for Assignment Model is given below:

→ Let, denotes the cost of resources 'i' to the task 'j'; such that

→ Now assignment problems are of the Minimization type. So, our objective function is to minimize the overall cost.
→ Subjected to constraint;
(i) For all task, only one resource is possible:
(ii) For all resource, there is only one task possible;
(iii) is '0' or '1'.
Types of Assignment Problem:
(i) Balanced Assignment Problem
- It consist of a suqare matrix (n x n).
- Number of rows = Number of columns
(ii) Unbalanced Assignment Problem
- It consist of a Non-square matrix.
- Number of rows Number of columns
Methods to solve Assignment Model:
(i) Integer Programming Method:
-
In assignment problem, either allocation is done to the cell or not.
-
So this can be formulated using 0 or 1 integer.
-
While using this method, we will have n x n decision varables, and n+n equalities.
-
So even for 4 x 4 matrix problem, it will have 16 decision variables and 8 equalities.
-
So this method becomes very lengthy and difficult to solve.
(ii) Transportation Methods:
-
As assignment problem is a special case of transportation problem, it can also be solved using transportation methods.
-
In transportation methods (NWCM, LCM & VAM), the total number of allocations will be (m+n-1) and the solution is known as non-degenerated. (For eg: for 3 x 3 matrix, there will be 3+3-1 = 5 allocations)
-
But, here in assignment problems, the matrix is a square matrix (m=n).
-
So total allocations should be (n+n-1), i.e. for 3 x 3 matrix, it should be (3+3-1) = 5
-
But, we know that in 3 x 3 assignment problem, maximum possible possible assignments are 3 only.
-
So, if are we will use transportation methods, then the solution will be degenerated as it does not satisfy the condition of (m+n-1) allocations.
-
So, the method becomes lengthy and time consuming.
(iii) Enumeration Method:
-
It is a simple trail and error type method.
-
Consider a 3 x 3 assignment problem. Here the assignments are done randomly and the total cost is found out.
-
For 3 x 3 matrix, the total possible trails are 3!
So total 3! = 3 x 2 x 1 = 6 trails are possible. -
The assignments which gives minimum cost is selected as optimal solution.
-
But, such trail and error becomes very difficult and lengthy.
-
If there are more number of rows and columns,
( For eg: For 6 x 6 matrix, there will be 6! trails. So 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720 trails possible)
then such methods can't be applied for solving assignments problems.
(iv) Hungarian Method:
-
It was developed by two mathematicians of Hungary. So, it is known as Hungarian Method.
-
It is also know as Reduced matrix method or Flood's technique.
-
There are two main conditions for applying Hungarian Method:
(1) Square Matrix (n x n).
(2) Problem should be of minimization type.
Suggested Notes:
Modified Distribution Method (MODI) | Transportation Problem | Transportation Model
Stepping Stone | Transportation Problem | Transportation Model
Vogel’s Approximation Method (VAM) | Method to Solve Transportation Problem | Transportation Model
Transportation Model - Introduction
North West Corner Method | Method to Solve Transportation Problem | Transportation Model
Least Cost Method | Method to Solve Transportation Problem | Transportation Model
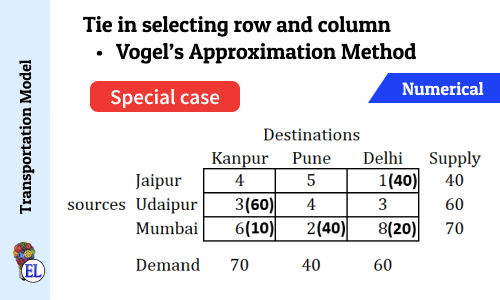
Tie in selecting row and column (Vogel's Approximation Method - VAM) | Numerical | Solving Transportation Problem | Transportation Model
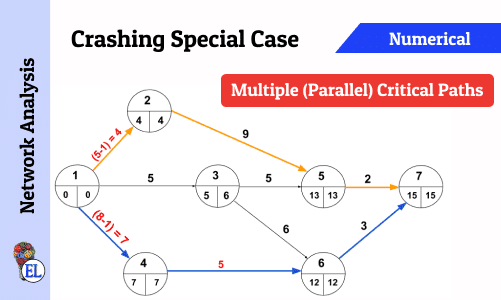
Crashing Special Case - Multiple (Parallel) Critical Paths
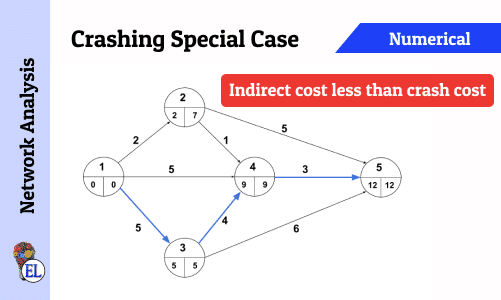
Crashing Special Case - Indirect cost less than Crash Cost

Basics of Program Evaluation and Review Technique (PERT)
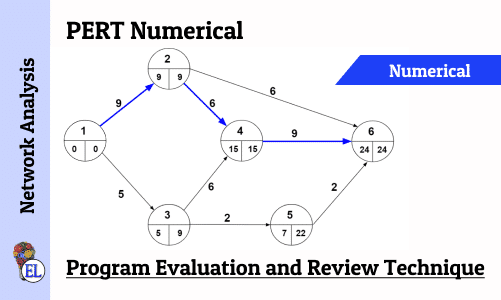
Numerical on PERT (Program Evaluation and Review Technique)
Network Analysis - Dealing with Network Construction Basics
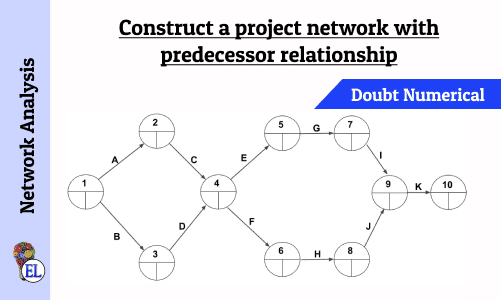
Construct a project network with predecessor relationship | Operation Research | Numerical
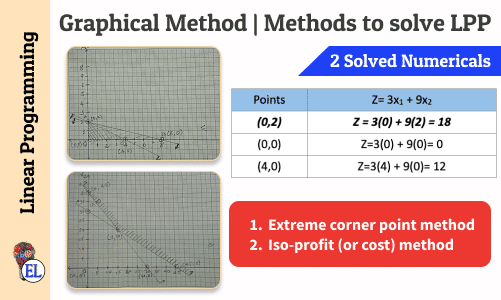
Graphical Method | Methods to solve LPP | Linear Programming
Basics of Linear Programming

Linear Programming Problem (LPP) Formulation with Numericals

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment