Critically Damped System (ξ = 1)
Watch videoComments
 Fig.1(Critically Damped System)
Fig.1(Critically Damped System)
- Critically damped system(ξ=1): If the damping factor
ξis equal to one, or the damping coefficientcis equal to critical damping coefficient "cc", then the system is said to be a critically damped system.
- Two roots for critically damped system are given by S1 and S2 as below:
- For ;
Here both the roots are real and equal, so the solution to the differential equation can be given by
- Now differentiating equation (1) with respect to ‘t’, we get:
-
Now, let at
:
: -
Substituting these values in equation (1):
- Same way, from equation (2), we get

- Now putting the values of A and B in equation (1), we get:
Conclusion
-
From above equation (5), it is seen that as time
tincreases, the displacementxdecreases exponentially. -
The motion of a critically damped system is aperiodic (aperiodic motion motions are those motions in which the motion does not repeat after a regular interval of time i.e non periodic motion) and so the system does not shows vibrations.
-
For critically damped systems, if a system is displaced from its initial position, it will try to reach its mean position in a very short time.
-
Critically damped systems are generally seen in hydraulic doors closer as it is necessary for the door to come to its initial position in a very short time.
Suggested Notes:

Law of Parallelogram of Forces : 5 in 5 MCQs S01-E01
Variation of Tractive Force | Tractive Effort | Effect of Partial Balancing of Locomotives
Balancing of V-Engines
Concept of Direct and Reverse Crank for V-engines & Radial engines
Static and Dynamic Balancing
Multi Cylinder Inline Engine (with firing order) | Numerical
Damped free Vibration - Numerical 1
Damped free Vibration - Numerical 2

Damped free Vibration - Numerical 4
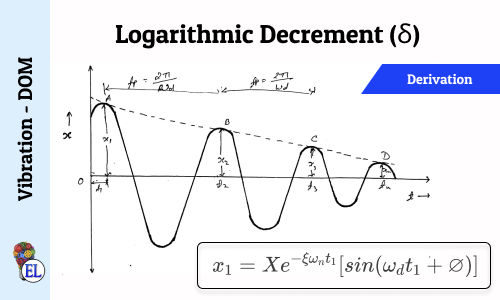
Logarithmic Decrement (δ)
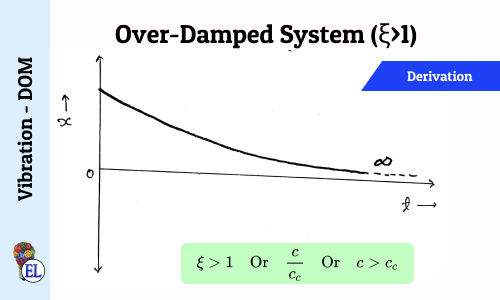
Over-Damped System (ξ>1)
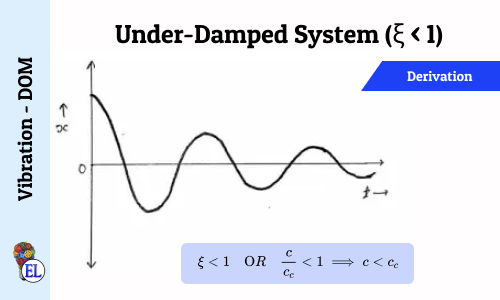
Under-Damped System (ξ < 1)

Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment