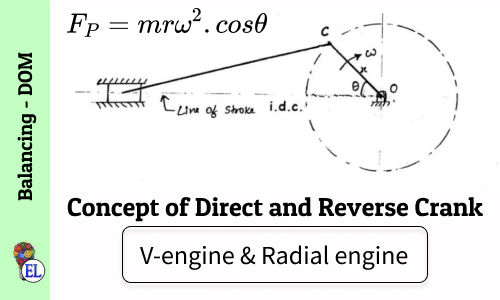
V-Engine
A V-engine is a two cylinder engine, which has a common crank and the axis of cylinder makes a "V" shape.
Since V-engines have a common crank and the crank revolves in one plane, there is no primary or secondary couple acting on the engine.
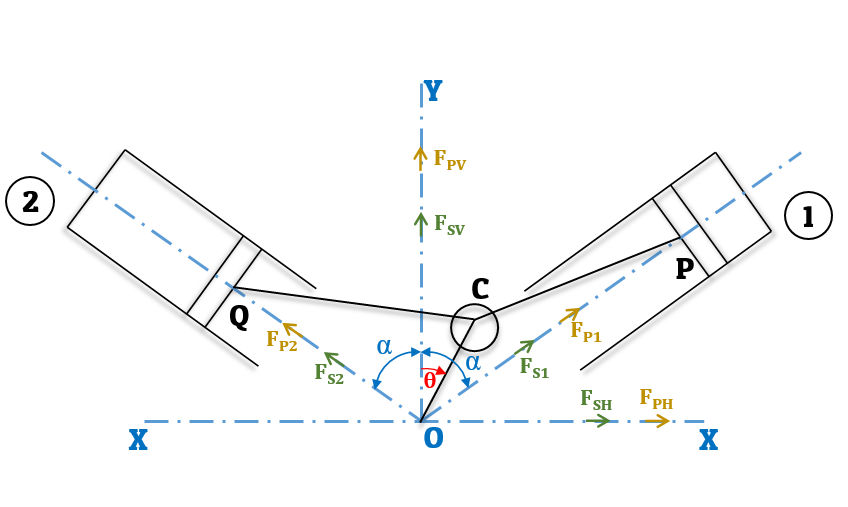
Consider a V-engine as shown in fig.1 having common crank OC and two connecting rods CP and CQ. The lines of stroke OP and OQ are inclined to vertical axis OY at an angle ‘α’.
Fig-1
Let,
m = mass of reciprocating parts per cylinder, kg l = length of connecting rod, m r = radius of crank, m n = Obliquity ratio = l / r θ = Crank angle, measured from vertical axis OY, at any instant ω = Angular velocity of crank, rad/s 2 α = V-angle i.e. angle between lines of strokes of two cylinders \begin{aligned}
m &= \text{mass of reciprocating parts per cylinder, kg}\\
l &= \text{length of connecting rod, m}\\
r &= \text{radius of crank, m}\\
n &= \text{Obliquity ratio }= l/r\\
θ &= \text{Crank angle, measured from vertical axis OY, at any instant}\\
ω &= \text{Angular velocity of crank, rad/s}\\
2 \alpha &= \text{V-angle i.e. angle between lines of strokes of two cylinders}\\
\end{aligned} m l r n θ ω 2 α = mass of reciprocating parts per cylinder, kg = length of connecting rod, m = radius of crank, m = Obliquity ratio = l / r = Crank angle, measured from vertical axis OY, at any instant = Angular velocity of crank, rad/s = V-angle i.e. angle between lines of strokes of two cylinders We know that,
Primary unbalanced force in single cylinder engine is,
F P = m r ω 2 cos θ F_P = mr\omega^2 \cos \theta F P = m r ω 2 cos θ
Secondary unbalanced force in single cylinder engine is,
F S = m r ω 2 ( cos 2 θ n ) F_S = mr\omega^2 \bigg({\cos2\theta \over n} \bigg) F S = m r ω 2 ( n cos 2 θ )
1. Primary forces (F P F_P F P
(i) Primary forces in individual cylinders:
F P 1 = m r ω 2 cos ( α − θ ) F P 2 = m r ω 2 cos ( α + θ ) F_{P1} = mr\omega^2 \cos (\alpha -\theta)\\
F_{P2} = mr\omega^2 \cos (\alpha +\theta) F P 1 = m r ω 2 cos ( α − θ ) F P 2 = m r ω 2 cos ( α + θ )
(ii) Total primary force along Y axis (F P V F_{PV} F P V
As both components ( F P 1 ⋅ cos α ) (F_{P1}\sdot \cos\alpha) ( F P 1 ⋅ cos α ) ( F P 2 ⋅ cos α ) (F_{P2} \sdot \cos\alpha) ( F P 2 ⋅ cos α )
F P V = F P 1 cos α + F P 2 cos α = m r ω 2 cos ( α − θ ) cos α − m r ω 2 cos ( α + θ ) cos α = m r ω 2 cos α [ cos ( α − θ ) + cos ( α + θ ) ] = m r ω 2 cos α ⋅ ( 2 cos θ cos α ) = 2 m r ω 2 cos 2 α cos θ \begin{aligned}
F_{PV} &= F_{P1} \cos\alpha + F_{P2} \cos\alpha\\
&= mr\omega^2 \cos (\alpha -\theta)\cos\alpha \ - mr\omega^2 \cos (\alpha +\theta)\cos\alpha\\
&= mr\omega^2 \cos\alpha [\cos (\alpha -\theta) + \cos (\alpha+\theta)]\\
&= mr\omega^2 \cos\alpha \sdot (2 \cos\theta \cos\alpha)\\
&= 2mr\omega^2 \cos^2\alpha \cos\theta
\end{aligned} F P V = F P 1 cos α + F P 2 cos α = m r ω 2 cos ( α − θ ) cos α − m r ω 2 cos ( α + θ ) cos α = m r ω 2 cos α [ cos ( α − θ ) + cos ( α + θ )] = m r ω 2 cos α ⋅ ( 2 cos θ cos α ) = 2 m r ω 2 cos 2 α cos θ (iii) Total primary force along X-axis (F P H F_{PH} F P H
As both components ( F P 1 ⋅ sin α ) (F_{P1} \sdot \sin \alpha) ( F P 1 ⋅ sin α ) ( F P 2 ⋅ sin α ) (F_{P2}\sdot \sin \alpha) ( F P 2 ⋅ sin α )
F P H = F P 1 sin α + F P 2 sin α = m r ω 2 cos ( α − θ ) sin α − m r ω 2 cos ( α + θ ) sin α = m r ω 2 sin α [ cos ( α − θ ) − cos ( α + θ ) ] = m r ω 2 sin α ⋅ ( 2 sin θ sin α ) = 2 m r ω 2 sin 2 α sin θ \begin{aligned}
F_{PH} &= F_{P1} \sin\alpha + F_{P2} \sin\alpha\\
&= mr\omega^2 \cos (\alpha -\theta)\sin\alpha \ - mr\omega^2 \cos (\alpha +\theta)\sin\alpha\\
&= mr\omega^2\sin\alpha [\cos (\alpha -\theta)-\cos (\alpha +\theta)]\\
&= mr\omega^2\sin\alpha \ \sdot (2\sin \theta \sin \alpha)\\
&= 2mr\omega^2\sin^2\alpha\sin \theta
\end{aligned} F P H = F P 1 sin α + F P 2 sin α = m r ω 2 cos ( α − θ ) sin α − m r ω 2 cos ( α + θ ) sin α = m r ω 2 sin α [ cos ( α − θ ) − cos ( α + θ )] = m r ω 2 sin α ⋅ ( 2 sin θ sin α ) = 2 m r ω 2 sin 2 α sin θ (iv) Resultant primary force (F p F_p F p
F p = ( F P V ) 2 + ( F P H ) 2 = ( 2 m r ω 2 cos 2 α cos θ ) 2 + ( 2 m r ω 2 sin 2 α sin θ ) 2 = 2 m r ω 2 ( cos 2 α cos θ ) 2 + ( sin 2 α sin θ ) 2 \begin{aligned}
F_p &= \sqrt{(F_{PV})^2 +(F_{PH})^2 }\\
&= \sqrt{(2mr\omega^2 \cos^2\alpha \cos\theta)^2 + (2mr\omega^2\sin^2\alpha\sin \theta)^2}\\
&= 2mr\omega^2\sqrt{(\cos^2\alpha \cos\theta)^2 + (\sin^2\alpha\sin \theta)^2}
\end{aligned} F p = ( F P V ) 2 + ( F P H ) 2 = ( 2 m r ω 2 cos 2 α cos θ ) 2 + ( 2 m r ω 2 sin 2 α sin θ ) 2 = 2 m r ω 2 ( cos 2 α cos θ ) 2 + ( sin 2 α sin θ ) 2 The angle made by resultant primary force with vertical axis is;
β P = tan − 1 ( F P H F P V ) = tan − 1 ( 2 m r ω 2 sin 2 α sin θ 2 m r ω 2 cos 2 α cos θ ) = tan − 1 ( tan 2 α ⋅ tan θ ) \begin{aligned}
\beta_P &= \tan^{-1} \bigg ( {F_{PH} \over F_{PV}}\bigg)\\
&= \tan^{-1} \bigg ( {2mr\omega^2\sin^2\alpha\sin \theta \over 2mr\omega^2 \cos^2\alpha \cos\theta} \bigg)\\
&= \tan^{-1} (\tan^2\alpha \ \sdot \ \tan\theta)
\end{aligned} β P = tan − 1 ( F P V F P H ) = tan − 1 ( 2 m r ω 2 cos 2 α cos θ 2 m r ω 2 sin 2 α sin θ ) = tan − 1 ( tan 2 α ⋅ tan θ )
2. Secondary forces (F S F_S F S
(i) Secondary forces in individual cylinder:
F S 1 = m r ω 2 cos 2 ( α − θ ) n F S 2 = m r ω 2 cos 2 ( α + θ ) n F_{S1} = mr \omega^2 {\cos2(\alpha-\theta) \over n}\\
F_{S2} = mr \omega^2 {\cos2(\alpha+\theta) \over n}\\ F S 1 = m r ω 2 n cos 2 ( α − θ ) F S 2 = m r ω 2 n cos 2 ( α + θ ) (ii) Total secondary force along Y axis (F S V F_{SV} F S V
As both components ( F S 1 ⋅ cos α ) (F_{S1}\sdot\cos \alpha) ( F S 1 ⋅ cos α ) ( F S 2 ⋅ cos α ) (F_{S2}\sdot \cos \alpha) ( F S 2 ⋅ cos α )
F S V = F S 1 cos α + F S 2 cos α = m r ω 2 cos 2 ( α − θ ) n cos α + m r ω 2 cos 2 ( α + θ ) n cos α = m r ω 2 cos α [ cos 2 ( α − θ ) n + cos 2 ( α + θ ) n ] = 1 n m r ω 2 cos α ⋅ [ 2 ⋅ cos 2 θ ⋅ cos 2 α ] = 2 n m r ω 2 cos α ⋅ cos 2 α ⋅ cos 2 θ \begin{aligned}
F_{SV} &= F_{S1} \cos \alpha + F_{S2} \cos \alpha\\
&= mr \omega^2 {\cos2(\alpha-\theta) \over n}\cos\alpha + mr \omega^2 {\cos2(\alpha+\theta) \over n}\cos\alpha\\
&= mr \omega^2\cos\alpha \bigg[{\cos2(\alpha-\theta) \over n} + {\cos2(\alpha+\theta) \over n}\bigg]\\
&={1\over n} mr \omega^2\cos\alpha \sdot[2\sdot\cos2\theta\sdot\cos2\alpha]\\
&= {2 \over n}mr \omega^2\cos\alpha\sdot\cos2\alpha\sdot\cos2\theta
\end{aligned} F S V = F S 1 cos α + F S 2 cos α = m r ω 2 n cos 2 ( α − θ ) cos α + m r ω 2 n cos 2 ( α + θ ) cos α = m r ω 2 cos α [ n cos 2 ( α − θ ) + n cos 2 ( α + θ ) ] = n 1 m r ω 2 cos α ⋅ [ 2 ⋅ cos 2 θ ⋅ cos 2 α ] = n 2 m r ω 2 cos α ⋅ cos 2 α ⋅ cos 2 θ (iii) Total secondary force along X-axis (F S H F_{SH} F S H
As both components ( F S 1 ⋅ sin α ) (F_{S1}\sdot\sin\alpha) ( F S 1 ⋅ sin α ) ( F S 2 ⋅ sin α ) (F_{S2}\sdot\sin\alpha) ( F S 2 ⋅ sin α )
F S H = F S 1 sin α − F S 2 sin α = m r ω 2 cos 2 ( α − θ ) n sin α − m r ω 2 cos 2 ( α + θ ) n sin α = m r ω 2 sin α [ cos 2 ( α − θ ) n − cos 2 ( α + θ ) n ] = 1 n m r ω 2 sin α ⋅ [ 2 ⋅ sin 2 θ ⋅ sin 2 α ] = 2 n m r ω 2 sin α ⋅ sin 2 α ⋅ sin 2 θ \begin{aligned}
F_{SH} &= F_{S1} \sin \alpha - F_{S2} \sin \alpha\\
&= mr \omega^2 {\cos2(\alpha-\theta) \over n}\sin\alpha - mr \omega^2 {\cos2(\alpha+\theta) \over n}\sin\alpha\\
&= mr \omega^2\sin\alpha \bigg[{\cos2(\alpha-\theta) \over n} - {\cos2(\alpha+\theta) \over n}\bigg]\\
&= {1\over n} mr \omega^2\sin\alpha \sdot[2\sdot\sin2\theta\sdot\sin2\alpha]\\
&= {2 \over n}mr \omega^2\sin\alpha\sdot\sin2\alpha\sdot\sin2\theta
\end{aligned} F S H = F S 1 sin α − F S 2 sin α = m r ω 2 n cos 2 ( α − θ ) sin α − m r ω 2 n cos 2 ( α + θ ) sin α = m r ω 2 sin α [ n cos 2 ( α − θ ) − n cos 2 ( α + θ ) ] = n 1 m r ω 2 sin α ⋅ [ 2 ⋅ sin 2 θ ⋅ sin 2 α ] = n 2 m r ω 2 sin α ⋅ sin 2 α ⋅ sin 2 θ (iv) Resultant secondary force (F S F_S F S
F s = ( F S V ) 2 + ( F S H ) 2 = ( 2 n m r ω 2 cos α ⋅ cos 2 α ⋅ cos 2 θ ) + ( 2 n m r ω 2 sin α ⋅ sin 2 α ⋅ sin 2 θ ) 2 = 2 n m r ω 2 ( cos α ⋅ cos 2 α ⋅ cos 2 θ ) 2 + ( sin α ⋅ sin 2 α ⋅ sin 2 θ ) 2 \begin{aligned}
F_s &= \sqrt{(F_{SV})^2 + (F_{SH})^2}\\
&= \sqrt{( {2 \over n}mr \omega^2\cos\alpha\sdot\cos2\alpha\sdot\cos2\theta)^ + ({2 \over n}mr \omega^2\sin\alpha\sdot\sin2\alpha\sdot\sin2\theta)^2}\\
&= {2 \over n} mr\omega^2 \sqrt{(\cos\alpha\sdot\cos2\alpha\sdot\cos2\theta)^2 + (\sin\alpha\sdot\sin2\alpha\sdot\sin2\theta)^2}
\end{aligned} F s = ( F S V ) 2 + ( F S H ) 2 = ( n 2 m r ω 2 cos α ⋅ cos 2 α ⋅ cos 2 θ ) + ( n 2 m r ω 2 sin α ⋅ sin 2 α ⋅ sin 2 θ ) 2 = n 2 m r ω 2 ( cos α ⋅ cos 2 α ⋅ cos 2 θ ) 2 + ( sin α ⋅ sin 2 α ⋅ sin 2 θ ) 2 The angle made by resultant secondary force with vertical axis is;
β S = tan − 1 ( F S H F S V ) = tan − 1 ( 2 n m r ω 2 sin α ⋅ sin 2 α ⋅ sin 2 θ 2 n m r ω 2 cos α ⋅ cos 2 α ⋅ cos 2 θ ) = tan − 1 ( tan α ⋅ tan 2 α ⋅ tan 2 θ ) \begin{aligned}
\beta_S &= \tan^{-1} \bigg( {F_{SH} \over F_{SV}}\bigg)\\
&= \tan^{-1} \bigg( {{2 \over n}mr \omega^2\sin\alpha\sdot\sin2\alpha\sdot\sin2\theta \over {2 \over n}mr \omega^2\cos\alpha\sdot\cos2\alpha\sdot\cos2\theta} \bigg)\\
&= \tan^{-1}\ (\tan\alpha \sdot \tan2\alpha \sdot \tan2\theta)
\end{aligned} β S = tan − 1 ( F S V F S H ) = tan − 1 ( n 2 m r ω 2 cos α ⋅ cos 2 α ⋅ cos 2 θ n 2 m r ω 2 sin α ⋅ sin 2 α ⋅ sin 2 θ ) = tan − 1 ( tan α ⋅ tan 2 α ⋅ tan 2 θ ) Advantages of V-engines
The design of V-engine is compact compared to multi-cylinder inline engines. So they consume less space.
Power output of V-engine is more compared to single cylinder engines because the crank receives power from both the cylinders.
The operation of V-engine is smoother for high speed performance.
Applications of V-engines
Because of its compactness, smoother operations and high power output, V-engines are used in sports cars.


Comments:
All comments that you add will await moderation. We'll publish all comments that are topic related, and adhere to our Code of Conduct.
Want to tell us something privately? Contact Us
Post comment